ГЛАВА 3. Физико-химические основы процессов взаимодействия активных частиц плазмы с поверхностью

4. Кинетика взаимодействия ХАЧ с поверхностью

При рассмотрении метода сложения сопротивлений в предыдущем разделе полагалось, что  взаимодействие ХАЧ с поверхностью состоит только из одной стадии – собственно химической реакции. Это являлось упрощением реальной ситуации, так как гетерогенное взаимодействие включает в себя три последовательные стадии - адсорбцию ХАЧ на поверхности, химическую реакцию и десорбцию образующихся продуктов реакции,  каждая из которых может быть лимитирующей. Другими словами, протекание процесса травления в кинетическом режиме строго означает лишь то, что его скорость не лимитируется объемными процессами. В то же время реальная кинетика процесса травления будет определяться закономерностями протекания наиболее медленной из трех названных гетерогенных стадий.

Для описания кинетики взаимодействия ХАЧ плазмы с поверхностью часто используется адсорбционно-десорбционная модель гетерогенного процесса, основанная на  теории активных центров Лангмюра-Хиншельвуда. Поверхность обрабатываемого материала рассматривается как совокупность активных центров – минимумов поверхностной энергии, способных присоединять (адсорбировать)  ХАЧ из объема плазмы. Попадающая на поверхность ХАЧ адсорбируется с вероятностью, зависящей от природы частиц, температуры и состояния поверхности. Далее, в зависимости от состояния поверхности, определяемого летучестью продуктов взаимодействия, могут реализоваться два направления последовательных процессов. В первом случае, если адсорбция ХАЧ происходит на свободных активных центрах, то в качестве следующего этапа будет выступать  процесс химического взаимодействия ХАЧ с поверхностью с образованием продуктов реакции.  Во втором случае, при адсорбции ХАЧ на слое продуктов реакции, происходит либо рекомбинация ХАЧ без взаимодействия с поверхностью, либо химическая реакция предваряется диффузией активных частиц через слой продукта. В качестве заключительной стадии следует рассматривать газификацию (десорбцию) продуктов взаимодействия, которая может быть спонтанной (термически активированной), либо требует дополнительной активации.

Адсорбция ХАЧ сорта  на поверхности :

(1)

может протекать по двум механизмам – физическому (физисорбция) и химическому (хемосорбция). Физисорбция является следствием слабых ван-дер-вальсовских сил притяжения между частицей и поверхностью. Процесс имеет слабо экзотермический характер с  ~ 1 – 25 кДж/моль, при этом глубина потенциальной ямы, отвечающей адсорбированному состоянию составляет  0.01 – 0.25 эВ. Из-за слабой связи с поверхностью адсорбированные частицы обладают высокой подвижностью – способностью к миграции. В отличии от физисорбции, хемосорбция сопровождается образованием химической связи между адсорбирующейся частицей и поверхностью. Процесс хемосорбции является сильно экзотермическим с  ~ 40 – 400 кДж/моль, что соответствует глубине потенциальной ямы  ~ 0.4 – 4 эВ. При хемосорбции молекул, атомы которых имеют двойные, тройные и т.д. связи, «присоединение» ХАЧ с поверхностью возникает с разрывом одной из этих связей

(2)

при этом разрушения молекулы не происходит. Если же атомы в исходной молекуле связаны одинарной связью,  то при хемосорбции может произойти распад молекулы

(3)

а процесс (3) носит название диссоциативной хемосорбции.  Во многих системах физический и химический  механизмы адсорбции реализуются параллельно, при этом конкретный режим процесса зависит от температуры поверхности и от формы потенциальных кривых, определяемых физико-химической природой поверхностных и адсорбируемых  частиц.

Для недиссоциативной адсорбции в термодинамически неравновесных системах вероятность адсорбции может быть определена из теории адсорбции Лангмюра как

(4)

где  - вероятность адсорбции при нулевой степени заполнения поверхности адсорбатом. Выражение (4) показывает, что хемосорбция прекратится при достижении условия   = 1 – это соответствует полному заполнению активных центров абсорбированными ХАЧ в количестве монослоя. Строго говоря, процесс на этом не останавливается, так как протекает физисорбция ХАЧ на хемосорбированном слое, в результате чего возможно накопление адсорбата на поверхности в количестве многих монослоев. Фактически же, в подавляющем большинстве случаев, физисорбция  компенсируется десорбционными процессами так, что  результирующий поток ХАЧ на поверхность становится равным нулю. Необходимо отметить также, что выражение (4) обычно дает заниженные значения для  в области средних степеней заполнения поверхности, так как не учитывает одного простого механизма: попадая на активный центр, занятый хемосорбированной ХАЧ, другая ХАЧ может сначала адсорбироваться на нем по физическому механизму, а затем мигрировать по поверхности до нахождения свободного активного центра.

Характер температурной зависимости   зависит от того, является ли переход от физисорбированного к хемосорбированному состоянию пороговым процессом. Если потенциальный барьер отсутствует, при низких температурах величина  близка к единице, но снижается с увеличением температуры  из-за снижения доли ХАЧ, которые при попадании на поверхность теряют достаточно энергии для того, чтобы быть захваченными в потенциальной яме адсорбированного состояния. В случае порогового процесса величина  очень мала до достижения условия ~ , а при дальнейшем увеличении температуры описывается аррениусовской зависимостью

(5)

где предэкспоненциальный множитель  снижается с ростом температуры по причине, указанной выше.

Экспериментальные измерения вероятности адсорбции при 300 К показывают, что диапазон этой величины очень широк 10^-6 – 1 и для данной системы «ХАЧ – поверхность» зависит от кристаллографической ориентации поверхности и ее шероховатости. Для многих поверхностей активными центрами при адсорбции являются поверхностные дефекты, такие как вакансии, краевые и винтовые дислокации и др. Химические активные газы (галогенсодержащие газы, кислород) и особенно радикалы, образующиеся при их диссоциации в плазме, адсорбируются на металлических поверхностях с высокими вероятностями с  ~ 0.1 – 1. При адсорбции атомов водорода на поверхности Si  ~ 1, однако для молекул H₂ эта величина не превышает нескольких процентов, а для молекул О₂ еще меньше – 10^-3 – 10^-4.

Десорбция представляет процесс обратный адсорбции. Предполагая, что процесс десорбции  протекает по первому кинетическому порядку

(6)

температурная зависимость константы скорости может быть представлена в аррениусовской форме

(7)

где  - это глубина потенциальной ямы соответствующего адсорбированного состояния ( или ). Величина  также зависит от механизма адсорбции и лежит в диапазоне 10¹⁴ – 10¹⁶ сек^-1 для физисорбции и 10¹³ – 10¹⁵ сек^-1 для хемосорбции (табл.1).  Альтернативой процессу (6) служит ассоциативная десорбция

(8)

которая описывается кинетическим уравнением второго порядка. Температурная зависимость коэффициента скорости качественно аналогична соотношению (7), а предэкспоненциальный множитель определяется как число столкновений между адсорбированными частицами в единицу времени на единице площади поверхности:

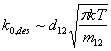(9)

где  и  - средний диаметр и приведенная масса сталкивающихся частиц:  и . Обычно для ассоциативной десорбции величина  лежит в диапазоне 10^-3–1 см²/сек.

Таблица 1

Параметры уравнения (7) при десорбции атомов галогенов

Примечание: * - поликристаллическая структура

В состоянии термодинамического равновесия скорости процессов  адсорбции и десорбции одинаковы. Предположим, что концентрация частиц сорта Aв газовой фазе составляет , а общий процесс описывается следующей схемой:

(10)

Обозначим через  поверхностную плотность центров адсорбции, тогда  - плотность центров адсорбции, покрытых адсорбированными молекулами, а величина  определяет количество свободных центров. Соответственно, для плотностей потоков адсорбирующихся и десорбирующихся частиц можно записать

(11)

(12)

Приравнивая  получим

(13)

(14)

где . Выражение (3.24) представляет собой уравнение изотермы адсорбции Лангмюра.

Рассмотрим теперь ситуацию, когда адсорбционно-десорбционные процессы сопровождаются химической реакцией ХАЧ с поверхностью. Простейшая схема такого процесса может быть представлена как

(15)

(16)

где индекс  соответствует нахождению частицы в газовой фазе. Стационарное балансное уравнение для степени заполнения поверхности частицами (включая адсорбированные ХАЧ и продукты взаимодействия) запишется в виде

(17)

а его решением будет

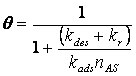(18)

где  - концентрация частиц  у поверхности. Последняя величина может быть найдена из условия равенства плотностей потоков частиц  из объема плазмы к поверхности и продуктов реакции с поверхности в газовую фазу:

(19)

где  - концентрация ХАЧ в объеме плазмы, а  и  - эффективная диффузионная длина и константа скорости диффузионной гибели нейтральных частиц, соответственно. Подходы к расчету  и  определяются диапазоном рабочих давлений реактора. В области высоких давлений, при  можно полагать , при этом . В области средних давлений, когда длина свободного пробега нейтральных частиц соизмерима с характерными размерами реактора, ( - объем рабочей камеры реактора,  - площадь внутренней поверхности), а . Для области низких давлений, при , транспорт частиц к поверхности не является диффузионным. В этом случае также имеем , но , где . Решая (19) относительно , подставляя результат в (18) и выражая скорость образования газообразного продукта  как  получим выражение, связывающее скорость целевого процесса с концентрацией ХАЧ в объеме плазмы. Данное выражение является достаточно громоздким, поэтому представление его в полном виде не наглядно и поэтому вряд ли целесообразно. Для наглядности рассмотрим два предельных случая, когда это уравнение трансформируется в более простые формы:

• Низкие давления: 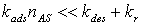. Для данного режима выражение (18) может быть переписано как 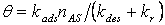 , откуда ясно, что 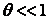. Скорость реакции описывается кинетическим уравнением первого порядка

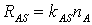
  , где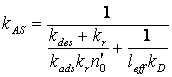

  (20)

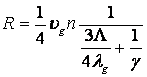
  (21)

  Нетрудно видеть, что уравнение (20) является аналогом соотношения (21), в котором все возможные кинетические характеристики взаимодействия были объединены в один макропараметр – вероятность взаимодействия 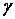. Очевидно также, что скорость реакции чувствительна к параметрам, определяющим концентрацию ХАЧ в газовой фазе – скорости потока газа через реактор, давлению газа и мощности, вкладываемой в разряд. Влияние процессов адсорбции и десорбции также может отражаться на энергии активации взаимодействия ХАЧ с поверхностью. Поэтому часто энергия активации химической реакции, определяемая из температурной зависимости скорости травления, является не истинной, а кажущейся. 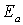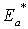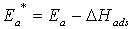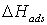Для случая, когда травление материала обеспечивается ХАЧ одного вида, которые слабо адсорбируются на поверхности и когда любые процессы с продуктами травления не являются тормозящими, связь между истинной  и кажущейся  энергиями активации определится как , где  - теплота адсорбции ХАЧ. 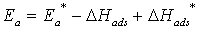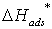Когда адсорбция ХАЧ слабая, а продукта реакции – сильная, то , где  - теплота адсорбции продукта реакции.

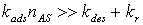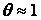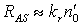• Высокие давления: . В этом режиме  и . Скорость реакции ХАЧ с поверхностью не зависит от концентрации ХАЧ в газовой фазе, то есть имеет нулевой кинетический порядок по концентрации ХАЧ в газовой фазе. Этот режим не является типичным для процессов плазмохимической обработки материалов в условиях ННГП.